二项堆 | Baeldung中文网

1. Introduction

In this tutorial, we’ll study binomial heaps. We use them to implement priority queues and discrete-event simulation for queuing systems.

2. Binomial Tree

A binomial heap is based on a binomial tree. So first, we’ll briefly introduce binomial trees.

2.1. Definition

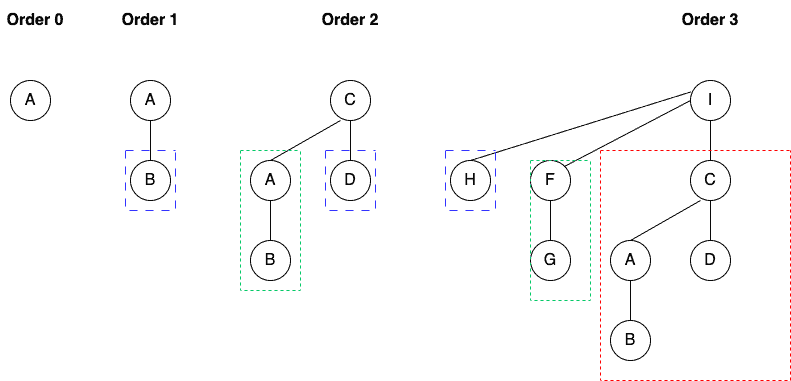
Formally, we can define a binomial tree B_k of order recursively:

For , $B_{0}$ contains only the root node .
For , the root of $B_{k}$ has roots of $B_{0}, B_{1}, \ldots, B_{k-1}$ as its children. So, contains root and binomial subtrees.

The root of the binomial tree $B_{k}$ has children (i.e., its degree is ), where the $i^{th}$ child ( $i=1,2,\ldots,k$ ) is again a binomial tree of order k-i :

As we see, it’s a recursive and ordered data structure.

A binomial tree of order has 2^k nodes, and its height is .

3. Binomial Heap

We define a binomial heap as a set of binomial trees satisfying the min-heap property.

That means that the value of each node is the minimum of the values in its sub-tree.

Further, we link root nodes of the binomial trees in the binomial heap to get a linked list $L_{H}$ .

3.1. Formal Definition

Formally, a binomial heap is a collection of binomial trees B_k such that:

Each binomial tree $B_{k}$ in has the min-heap property (is heap-ordered).
For each $k=0,1,2,\ldots$ , contains at most one binomial tree of order .

The first property tells us the minimal elements of the trees are in the linked list. The second property tells us that a binomial heap $\boldsymbol{H}$ with $\boldsymbol{n}$ nodes has $\lfloor \log n \rfloor + 1$ binomial trees.

3.2. Example

Let’s check out an example:

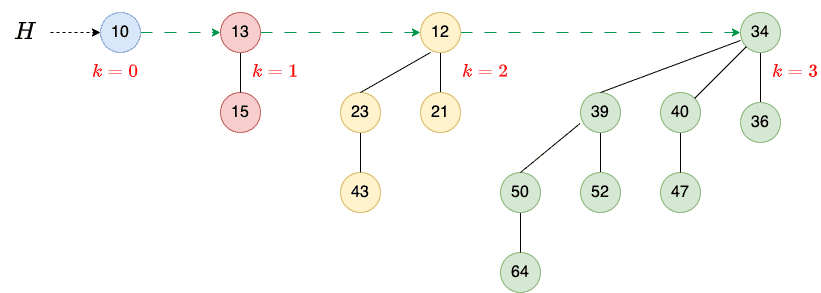
Binomial Heap

Here, the heap (15 nodes) consists of four binomial trees: $B_{0}$ (1 node), $B_{1}$ (2 nodes), $B_{2}$ (4 nodes), and $B_{3}$ (8 nodes).

Each binomial tree is heap-ordered, and the trees’ orders are unique. We can also see a linked list containing the root nodes in the increasing order of their degrees.

4. Operations

Let’s learn the basic operations we can perform on a binomial heap:

Create a new binomial heap
Find the minimum key
Merge two heaps
Insert a key

A binomial heap has other interesting operations, e.g., deleting a node, extracting a node with a minimum key, and changing the key of a particular node. However, we won’t cover them in this tutorial.

4.1. The Node Data Structure

We can represent each node in the binomial heap with the following data structure:

a variable KEY to store the node’s content (key)
a pointer PARENT to hold the link to its parent
a pointer CHILD to keep the link to its leftmost child
a pointer SIBLING to the leftmost child’s first right sibling
an integer DEGREE to store its degree

We can implement the heap without PARENT and DEGREE, but they make the algorithms for the operations easier to understand and formulate.

Additionally, we’ll use HEAD to point to the leftmost binomial tree of the heap . Each node in the binomial tree in a heap keeps track of all its children. For instance:

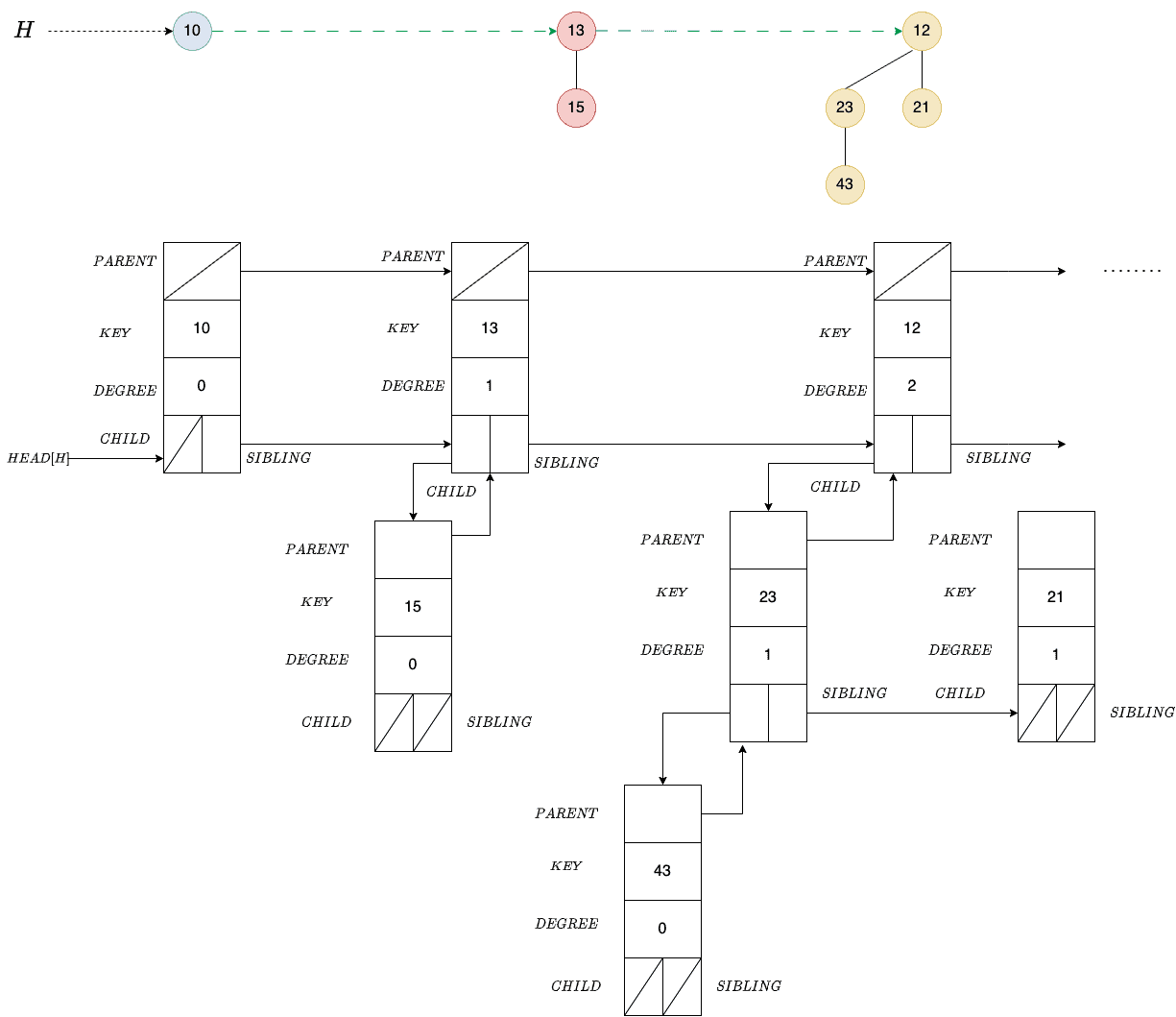
Binomial Heap Representation

The parent pointers of the root and child and sibling pointers of the leaves are empty. The sibling pointer of a root points to the next tree’s root.

4.2. Make an Empty Heap

To create an empty heap, we allocate the memory for the head node and set the pointers to empty values (usually denoted as $\varnothing$ , NIL, or NULL in textbooks).

This is an O(1) operation regarding space and time.

4.3. Find the Minimum Key

We already know that the root of a binomial tree in a binomial heap contains the tree’s minimum key.

Since the roots are in a linked list, we must traverse it to find the minimum.

This operation’s time complexity is $O(\log n)$ , where is the total number of nodes in the binomial heap . This is so because a binomial heap with nodes has at most $\log_2 n + 1$ trees.

5. Merge Two Heaps

Let H_1 and H_2 be two binomial heaps with n_1 and n_2 nodes.

5.1. Merging Two Binomial Trees of the Same Order

We’ll use a helper method of merging two binomial trees of the same degree. The result of merging two trees of order $\boldsymbol{k}$ is a tree of order $\boldsymbol{k+1}$ :

algorithm MergeBinomialTree(T1, T2):
    // INPUT
    //    T1 = binomial tree of the order k
    //    T2 = binomial tree of the order k
    // OUTPUT
    //    binomial tree of the order k+1 with total nodes as sum of nodes of T1 and T2

    // get root nodes of both trees
    R1 <- ROOT(T1)
    R2 <- ROOT(T2)

    // Make a tree with the larger key a child of the other tree to keep the min-heap property
    if KEY(R1) >= KEY(R2):
        R2 <- PARENT(R1)
        SIBLING(R1) <- CHILD(R2)
        CHILD(R2) <- R1
        DEGREE(R2) <- DEGREE(R2) + 1
        
        return T2
    else:
        R1 <- PARENT(R2)
        SIBLING(R2) <- CHILD(R1)
        CHILD(R1) <- R2
        DEGREE(R1) <- DEGREE(R1) + 1 
        
        return T1

We first compare the root nodes’ keys. To keep the min-heap property, the root with a smaller key should become the parent of the other tree’s root.

Since we use a fixed number of pointers and variables in a node structure, this operation has a constant time complexity O(1) .

5.2. Merging Two Heaps

The idea is to merge the sorted root lists of the input heaps H_1 and H_2 so that it’s also sorted. We can do that using MergeSort for sorted linked lists. Then, we traverse the list merging the successive pairs of roots with the same degree to make sure the resulting heap has at most one tree of any particular order:

algorithm MergeBinomialHeaps(H1, H2):
    // INPUT
    //    H1 = the first binomial heap
    //    H2 = the second binomial heap
    // OUTPUT
    //    H = the merged heap

    LH <- merge the root lists of H1 and H2 into a linked list sorted in non-decreasing order

    if LH is empty:
        return an empty heap

    // Start with the beginning of the list
    current <- the first node in LH
    next <- SIBLING(current)

    // Traverse LH merging the successive pairs of the root nodes with the same degrees
    while next != null:
        if DEGREE(current) != DEGREE(next):
            if DEGREE(current) > DEGREE(next):
                // Fix the nodes that are out of order
                Switch current and next
            // Move on to the next pair
            current <- next
            next <- SIBLING(current)
        else:
            // The current and next nodes have the same degree, so we merge their trees
            SIBLING(current) <- SIBLING(next)
            current <- the root of the tree we get by merging next and current
            next <- SIBLING(current)
    H <- the head of the heap whose root list is LH
    return H

The list L_H is sorted in the non-decreasing order. For any possible degree, it contains at most two roots of that degree. Furthermore, any two roots with the same degree will be next to each other in the list.

In each while loop iteration, we examine the degrees of two neighboring roots ( current and next ) and merge their trees if they’re equal. If so, we store the resulting tree’s root in the place of the left neighbor.

Otherwise, we check if the left neighbor has a greater degree than the right one. This can happen if the degree sequence contains the pattern $k \rightarrow k \rightarrow k+1 \rightarrow k+1$ :

We merge the first two roots to get $k+1 \rightarrow k+1 \rightarrow k+1$
Then, we get $k+2 \rightarrow k+1$
To maintain the order, we switch the roots to get $k+1 \rightarrow k+2$

Without switching, we won’t correctly merge the trees if the first degree after the pattern is k+2 . So, for example, we would have $k+2 \rightarrow k+1 \rightarrow k+2$ and miss merging the k+1 trees if we don’t switch the first two in the triple.

5.3. Example

Let’s understand the Merge operation with an example. So, we have two heaps:

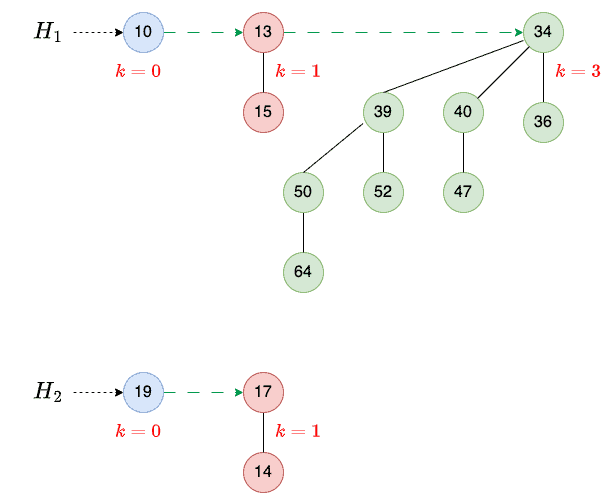
Binomial Heap Merge Original

We first look at H_1 and H_2 to find binomial trees of order 0. We combine them to get a binomial tree of order 1 (step 1). Then, we combine trees of order 1 to get a tree of order 2 (step 2). There’s only one tree of order 3, so we add it to the new heap:

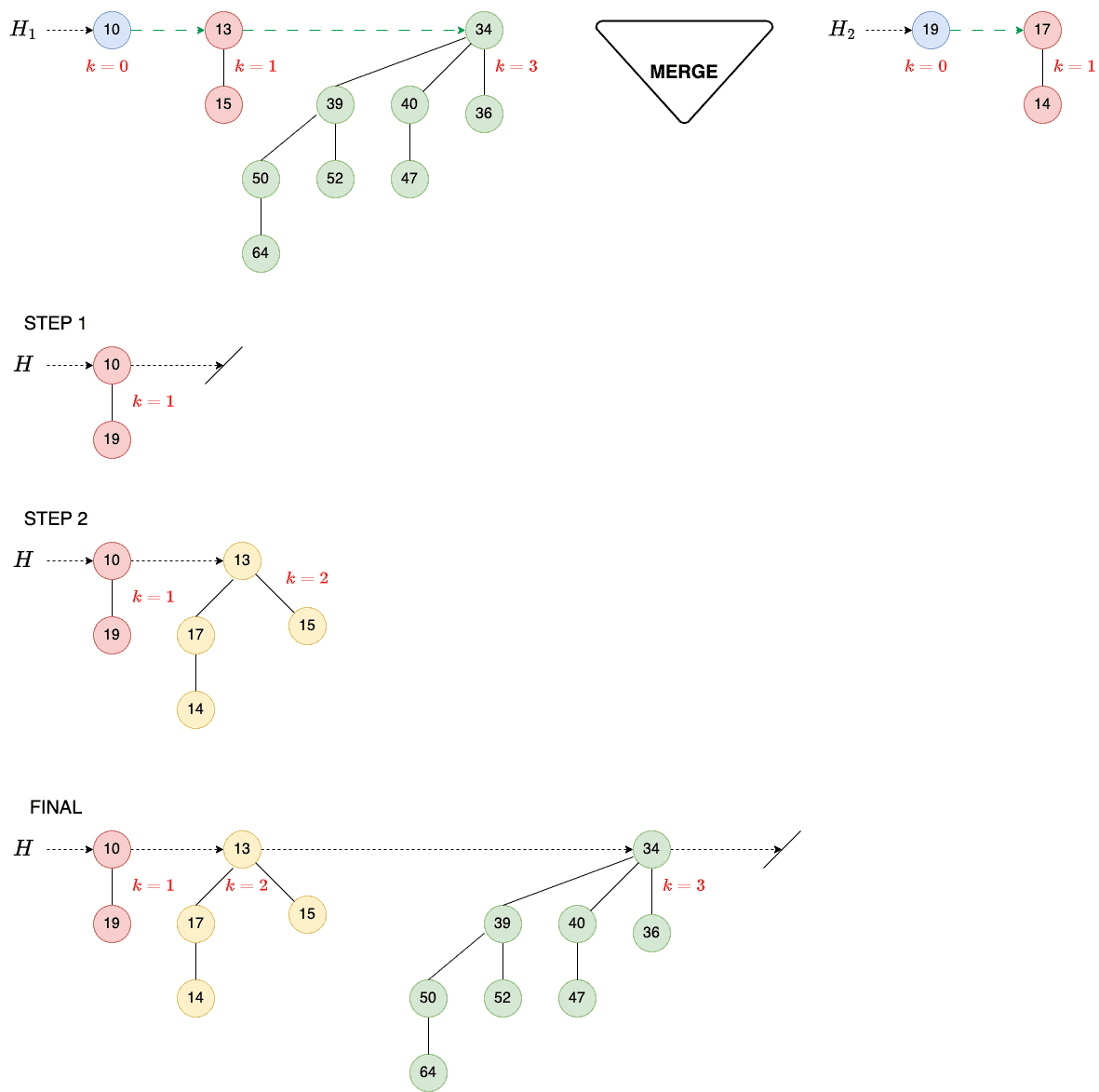
Binomial Heap Merge Flow

So, our final heap contains three trees of orders 1, 2, and 3.

5.4. Complexity

Our heaps H_1 and H_2 have n_1 and n_2 nodes. The resulting heap $\boldsymbol{H}$ has $\boldsymbol{n_1+n_2}$ nodes.

Now, H_1 contains at most $\log_2 n_1 + 1$ trees and H_2 contains at most $\log_2 n_2 + 1$ trees, so will contain at most $\boldsymbol{\log_2 n_1 + \log_2 n_2 + 2}$ trees.

Merging the sorted lists takes $O(\log n_1 + \log n_2)$ time. Since no more than $\log_2 n_1 + \log_2 n_2 + 1$ mergers, switches, and pointer movements are possible, the worst-case time complexity is $\boldsymbol{O(\log n_1 + \log n_2)=O(\log (n_1 + n _2)}$ .

The right-hand side follows from taking the logarithms of:

$[(n_1 + n_2)^2 \geq n_1 \times n_2]$

6. Insert a Key

To insert a new key into , we first initialize a new node () and set its key to . Then, we create a one-node binomial heap H_1 with as its root and merge it with :

algorithm InsertKeyIntoHeap(H, x):
    // INPUT
    //    H = the binomial heap
    //    x = the new key to be inserted
    // OUTPUT
    //    H with x inserted

    H1 <- make a new heap containing only a node with x as its key
    
    H <- merge H and H1
    
    Delete H1

    return H

We complete the procedure by deleting the temporary binomial heap H_1 , i.e., freeing its memory.

6.1. Complexity

This operation’s time and space complexity is governed by the time and space complexity of merging two heaps.

For the insert, we have n_1=n and n_2 =1. Thus, its time complexity is $O(\log n)$ , and its space complexity is O(n) .

6.2. Example

Let’s add a node with key 11 to our heap . So, we first assign memory and create node :

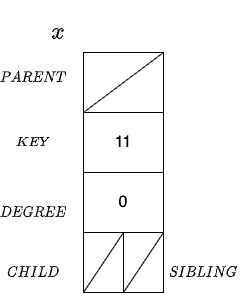
Step 1

Then, we create an empty heap H_1 and set its head to node x:

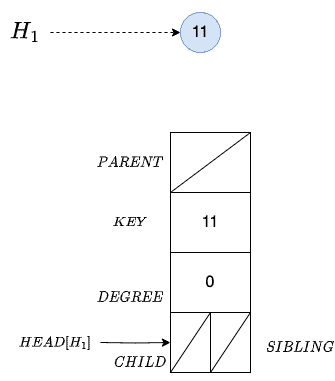
Step 2
As a result, we now have two heaps, and H_1 :

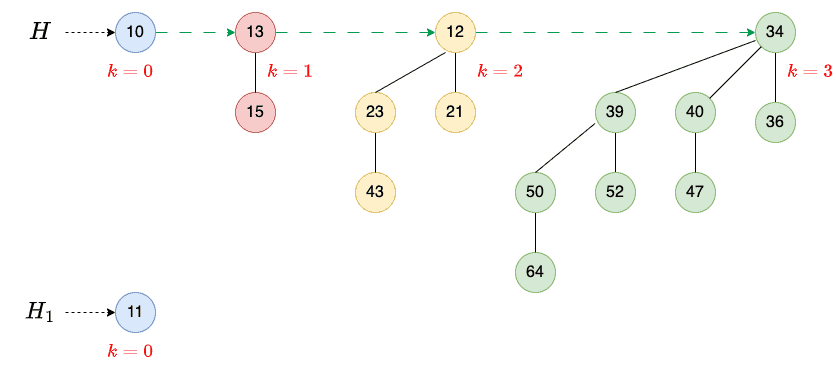
Binomial Heap Insert 1

Then, we merge them:

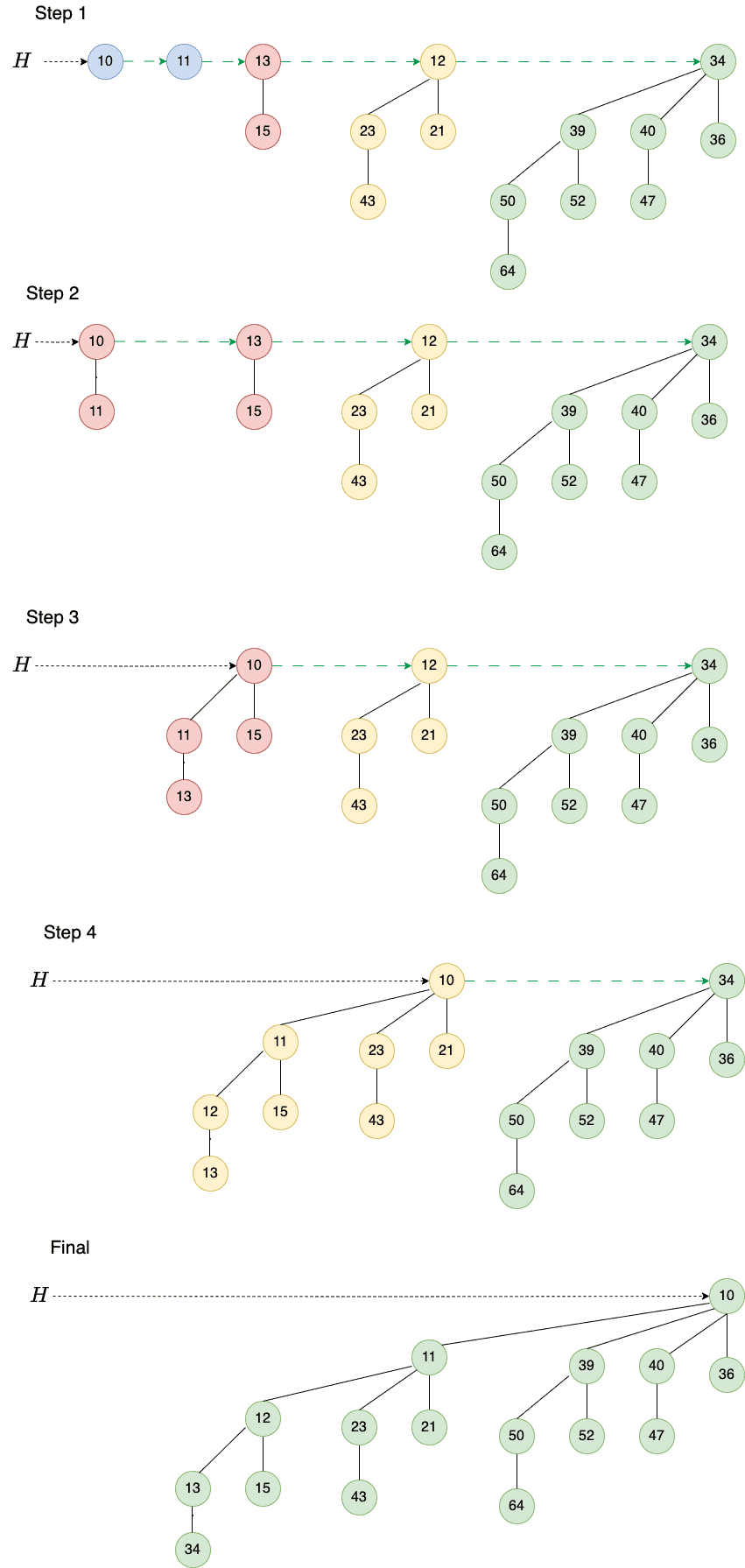
Binomial Heap Insert Steps

The result is a binomial heap containing a single binomial tree of order 4.

7. Binary Heap vs. Binomial Heap

A binary heap with height $h=\log_2 n$ is a binary tree that can hold any number of elements up to :

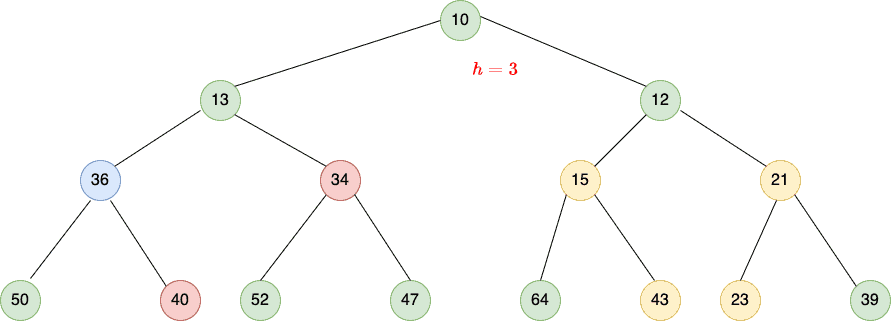
Binary Heap

On the other hand, a binomial heap is a collection of smaller binomial trees where the number of elements in a binomial tree of order is 2^k . So, we know the number of nodes in the binomial tree without looking into it.

Further, the merge operation for two binomial heaps with nodes and with nodes has the complexity of $\boldsymbol{O(\log (n_1 + n_2)}$ . This is faster than that of a binary heap ( $\boldsymbol{O(n_1 + n_2)}$ with the same number of nodes).

On the flip side, finding the minimum key in a binary heap is a constant-time operation since the root of a binary heap always contains the minimum key. In contrast, we need to search a list of roots in a binomial heap to find the minimum.

8. Conclusion

In this article, we explained binomial heaps and their properties and studied the operations we can perform on them.

We primarily use binomial heaps to implement priority queues. We merge them more efficiently than binary heaps, although finding the minimum in a binary heap is faster.

Persistence

REST

Security