1. 引言
在本教程中,我们将探讨 期望最大化(Expectation-Maximization, EM) 算法 —— 一种用于估计概率模型参数的非常流行的技术,也是 隐马尔可夫模型(HMM)、高斯混合模型(GMM)、卡尔曼滤波器等 背后的重要算法。
EM 特别适用于以下场景:
✅ 数据不完整
✅ 存在缺失值
✅ 存在未观测到的潜在变量(latent variables)
因此,EM 是每位数据科学家都应掌握的重要工具之一。
2. 似然函数
当我们估计一个模型的参数时,通常希望找到一组参数,使得这些参数“最贴合”我们的数据。换句话说,如果我们用这些参数训练模型并从中采样,采样结果应尽可能接近我们实际拥有的数据。
我们通过一个函数来描述这种“贴合度”——这就是 似然函数(Likelihood Function)。它以参数组合 为输入,输出我们观察到数据
的概率:
$$ L(\boldsymbol{\theta} ; \mathbf{X}) = p(\mathbf{X} \mid \boldsymbol{\theta}) $$
我们通常希望最大化这个似然函数,以找到最佳参数组合,这被称为 最大似然估计(Maximum Likelihood Estimation, MLE)。
但如果我们的数据中存在一个无法观测的潜在变量 ,事情就变得复杂了。此时似然函数变为:
$$ L(\boldsymbol{\theta} ; \mathbf{X}) = p(\mathbf{X} \mid \boldsymbol{\theta}) = \int p(\mathbf{X}, \mathbf{Z} \mid \boldsymbol{\theta}) d\mathbf{Z} $$
这个积分形式使得我们无法直接解析求解最优参数。这时,EM 算法就能派上用场了。
3. 直观的抛硬币示例
假设我们有两个硬币 A 和 B,它们正面朝上的概率分别是未知的 和
。我们想通过实验估计这两个参数。
在实验中,我们每次随机选择一个硬币抛 10 次,并重复 5 次:
| 抛掷序列 | 使用的硬币 | 正面次数 | 反面次数 |
|---|---|---|---|
| HTTTHHTHTH | B | 0 | 5 |
| HHHHTHHHHH | A | 9 | 0 |
| HTHHHHHHTHH | A | 8 | 0 |
| HTHTTTHHTT | B | 0 | 4 |
| THHHTHHHTH | A | 7 | 0 |
如果我们知道每次使用的是哪个硬币,那么估计参数就很简单:
$$ \boldsymbol{\theta_A} = \frac{24}{30} = 0.8 \quad \text{(共 24 次正面,30 次抛掷)} $$ $$ \boldsymbol{\theta_B} = \frac{9}{20} = 0.45 \quad \text{(共 9 次正面,20 次抛掷)} $$
但如果我们丢失了硬币标识信息,只保留了抛掷结果,那么我们就无法直接知道哪次是哪个硬币抛的。这时问题就变成了一个典型的含有潜在变量的问题,EM 算法就能帮助我们解决这个问题。
4. 使用 EM 算法求解
EM 算法分为两个步骤,交替进行:
- E 步(期望步):估计潜在变量的期望值(即每组抛掷数据最可能来自哪个硬币)。
- M 步(最大化步):根据 E 步估计的期望值,重新估计参数
和
。
我们以一个初始猜测开始,比如: $$ \boldsymbol{\theta_A} = 0.6, \quad \boldsymbol{\theta_B} = 0.5 $$
然后:
E 步:估计硬币归属概率
对于每组抛掷结果(如 HHHHHTTTTT),我们计算它由 A 或 B 生成的概率:
$$ P(E \mid Z_A) = \binom{n}{x} \theta_A^x (1 - \theta_A)^{n - x} $$ $$ P(E \mid Z_B) = \binom{n}{x} \theta_B^x (1 - \theta_B)^{n - x} $$
再通过贝叶斯定理计算每组数据属于 A 或 B 的概率:
$$ P(Z_A \mid E) = \frac{P(E \mid Z_A) P(Z_A)}{P(E \mid Z_A) P(Z_A) + P(E \mid Z_B) P(Z_B)} $$
$$ P(Z_B \mid E) = \frac{P(E \mid Z_B) P(Z_B)}{P(E \mid Z_A) P(Z_A) + P(E \mid Z_B) P(Z_B)} $$
我们用这些概率对每组数据中的正面和反面进行加权分配。
M 步:更新参数估计
使用 E 步中得到的期望值重新估计 和
:
$$ \theta_A^1 = \frac{\text{A 的期望正面数总和}}{\text{A 的期望正反面总数}} = \frac{21.3}{21.3 + 8.6} = 0.71 $$ $$ \theta_B^1 = \frac{11.7}{11.7 + 8.4} = 0.58 $$
这些值比初始猜测更接近真实值。我们重复 E 步和 M 步,直到参数收敛。
5. 算法推导原理
EM 算法的核心在于最大化 不完整数据下的似然函数:
$$ \sum_{i=1}^{N} \log \left( \int p(\mathbf{X}, \mathbf{Z} \mid \boldsymbol{\theta}) d\mathbf{Z} \right) $$
由于积分在 log 内部,难以直接优化。我们引入一个辅助函数:
$$ \sum_{i=1}^{N} \log \left( \int f(Z) \cdot \frac{p(\mathbf{X}, \mathbf{Z} \mid \boldsymbol{\theta})}{f(Z)} d\mathbf{Z} \right) $$
利用 Jensen 不等式,我们可以将这个式子转化为一个下界:
$$ \sum_{i=1}^{N} \int f(Z) \log \left( \frac{p(\mathbf{X}, \mathbf{Z} \mid \boldsymbol{\theta})}{f(Z)} \right) d\mathbf{Z} $$
最优的 是后验概率
,即:
$$ f(Z) = P(Z \mid \mathbf{X}, \boldsymbol{\theta}) $$
这导致我们只能通过迭代来估计:先用当前参数估计后验概率(E 步),再用该后验估计参数(M 步)。
6. 算法流程图
我们可以通过一个流程图来总结整个 EM 算法的流程:
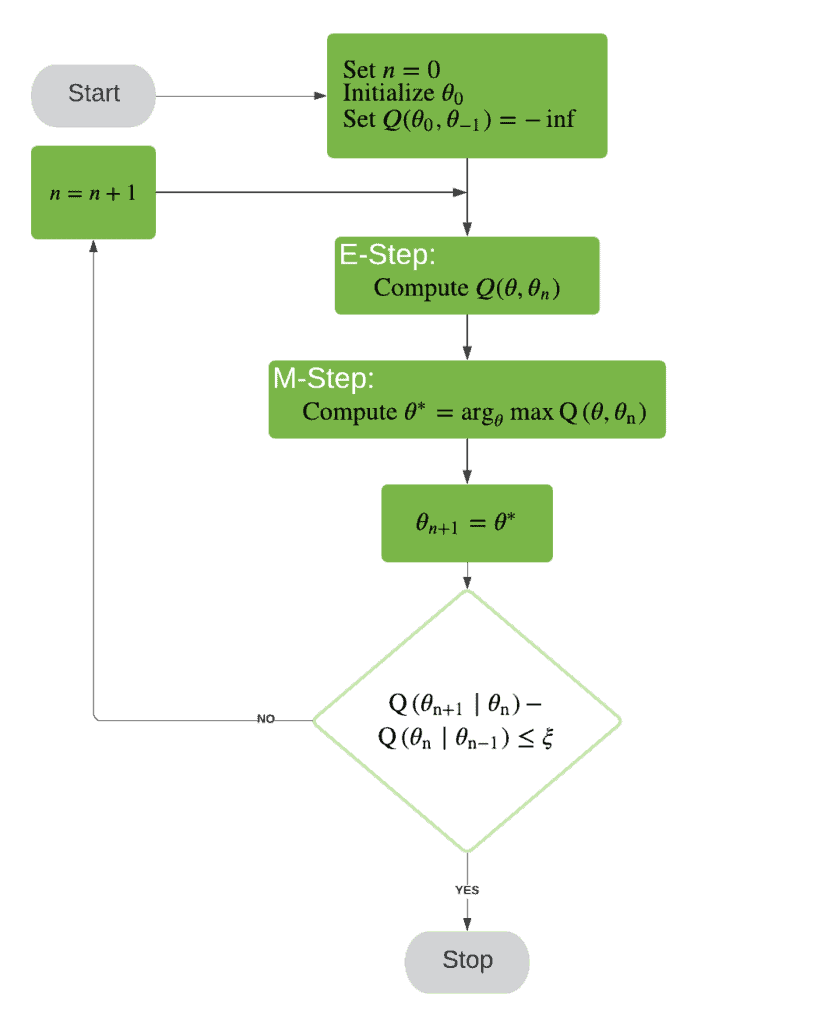
7. 总结
在本文中,我们:
- 回顾了最大似然估计(MLE)的基本概念
- 通过一个抛硬币的直观例子介绍了 EM 算法
- 推导了 EM 的数学基础,理解了其收敛保证
- 通过流程图总结了整个算法流程
EM 算法通过交替估计潜在变量和模型参数,逐步逼近最优解。虽然不能保证全局最优,但其稳定性和适用性使其成为处理不完全数据的强大工具。