门格定理 | Baeldung中文网

1. Introduction

In this tutorial, we’ll study Menger’s theorem on finite graphs. We define a graph with vertex set and edge set as finite when both sets are finite.

2. Menger’s Theorem

Karl Menger formulated this theorem in the year 1927 while he was studying graph connectivity problems. It was the pioneering work in that era because it paved the way for advanced theorems in graph connectivity (max-flow min-cut, strongly connected components) and duality in linear programming.

Let’s consider a finite undirected planar graph G=(V, E) . Here, we choose two non-adjacent vertices and from :

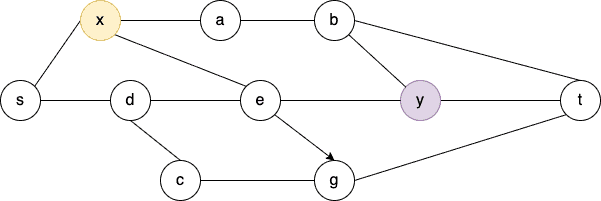
Graph1

Now, we want to disconnect from . So, how can we do it?

For this, we first need to find out how many internally disjoint paths there are between both and :

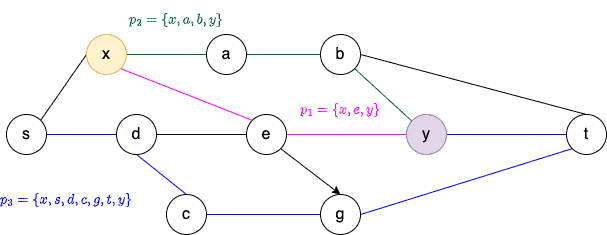
disjoint paths

If we have 3 disjoint paths p_1 , p_2 , and p_3 between them, then we can completely disconnect and by removing all edges on p_1 , p_2 , and p_3 :

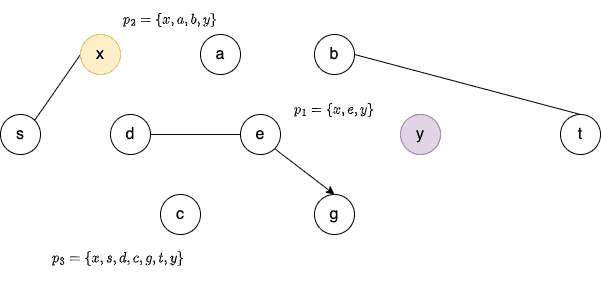
3 disjoint paths

Menger’s theorem is about the number of nodes and edges we need to remove from a graph to disconnect two non-adjacent vertices.

3. Formal Definition

It has two formulations: the vertex and edge versions.

3.1. The Vertex Case

Let and be distinct non-adjacent vertices in a connected graph G(V, E) .

Further, we define a vertex subset $S^{V}_{u,v}$ as a vertex-separator if the vertices and are in different components of the sub-graph $G-S^{V}_{u,v}$ (the sub-graph we get by removing from all the nodes $S^{V}_{u,v}$ and the associated edges).

This also means there’s no path from to in $G-S^{V}_{u,v}$ . Thus, $S^{V}_{u,v}$ separates from in . We call $S^{V}_{u,v}$ a vertex-cut.

The vertex case of Menger’s theorem states that for any undirected graph and non-adjacent vertices and , the minimum number of vertices in a vertex-cut is equal to the maximum number of pairwise internally disjoint paths between and .

3.2. The Edge Case

The edge case is similar.

We define $S^{E}_{u,v} \subseteq E$ as a edge-separator if the vertices and lie in different components of the sub-graph $G-S^{E}_{u,v}$ (sub-graph obtained after deleting $S^{E}_{u,v}$ from ). By analogy with the vertex case, we also call it an edge cut.

The edge version of Menger’s theorem states that for any undirected graph and non-adjacent vertices and , the number of edges in the minimum edge-cut for and is equal to the maximum number of pairwise edge-disjoint paths from to .

3.3. Example

We now move on to an example to understand these definitions. Here, we have a graph :

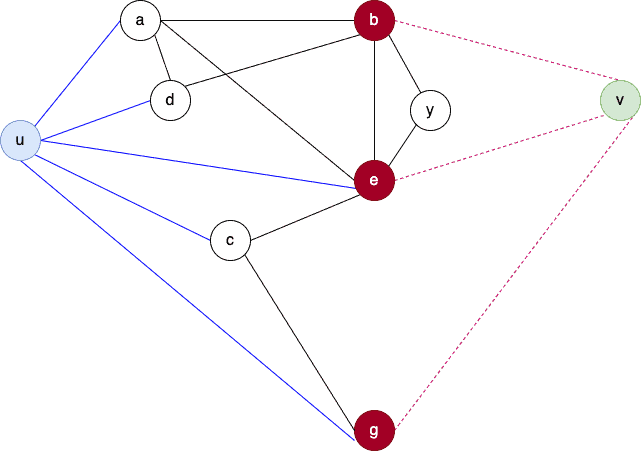
Graph Example

The set $S^{V}_{u,v} = \{b, e, g\}$ (red nodes) is the minimum vertex-cut, and the edge set $S^{E}_{u,v} =\{(b, v), (e,v), (g,v)\}$ (dashed pink) is the minimum edge-cut.

They correspond to a three-element set of internal disjoint paths (paths that don’t share any vertex other than and ) $P=\{\{ (u, a), (a, b), (b, v)\}, \{(u, e), (e, v)\}, \{(u, g), (g, v)\} \}$ .

No larger set of paths is disjoint internally and connects and . So, the theorem works: the minimal edge and vertex cuts have the same cardinality as the maximum disjoint path set.

4. Proof of Menger’s Theorem

We’ll use induction on the number of edges to prove the theorem.

To improve exposition, we define as the set of all neighbors of and as the set of all neighboring vertices to .

4.1. Base Case

For with no edges, the minimum separator is the set of common vertices of and .

The vertices in $A \cap B$ correspond to paths between and , which proves the base case.

4.2. Induction

Let’s say our graph has m > 0 edges and assume that Menger’s Theorem holds for all graphs with edges.

We aim to prove that the maximum number of independent paths between and equals , the size of the minimum cut in .

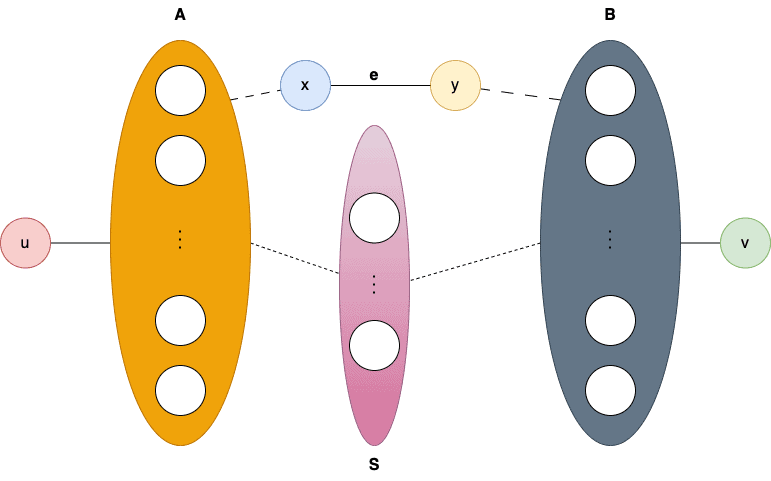
To do so, let e=(x, y) be an edge in , and let be the minimum vertex cut in G'=G - e : The proof of Menger's Theorem.

If has vertices, it’s the minimum cut for . Since has m-1 edges and Menger’s theorem holds for it by the inductive hypothesis, it also holds for .

Otherwise, has k-1 vertices. Why? That’s because if it had fewer nodes, the minimum cut in would also have fewer than vertices, which is a contradiction.

Now, each path in is:

either an path in (so it doesn’t contain the edge )
or a path containing

The minimum separator of and $S\cup\{x\}$ is also the minimum separator of and and has vertices. So, there are paths from to $S\cup\{x\}$ . The same goes for and $S\cup\{y\}$ . Concatenating those paths, we get at most paths from to , which we wanted to prove: k-1 without and one through .

5. Max-flow Min-cut Theorem for Network Flow

The max-flow min-cut theorem is the generalized version of Menger’s theorem.

In graph and optimization theory, the max-flow min-cut theorem states that in a flow network created from a directed acyclic graph, the maximum amount of flow that can pass from the source node to the sink node is equal to the total weight of the edges in the minimum cut.

Let’s understand this with an example. So, we have a directed acyclic graph whose each has a flow and a capacity:

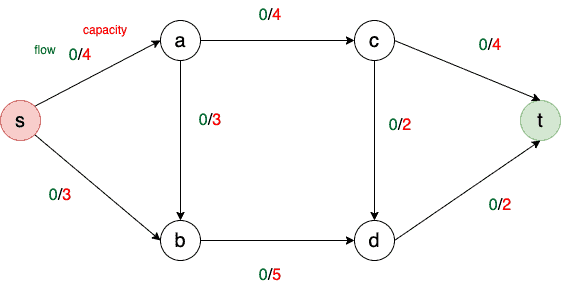
Network Flow

The flow is the quantity of load (processing power, network requests, etc.) we are currently transporting over that edge, and the capacity is the maximum load.

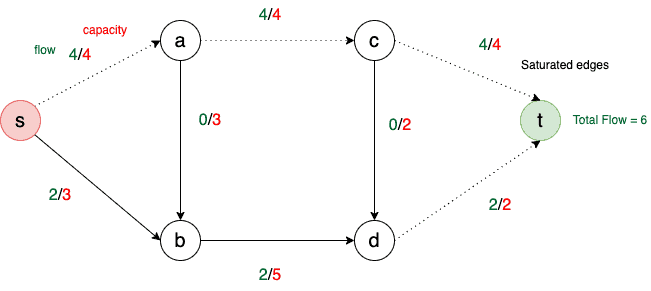
Initially, we set the flow over all edges to 0. Now, we have two minimum s-t edge separators: $S_1=\{(s, a), (s, b)\}$ , and $S_2=\{(c, t), (d, t)\}$ . But, S_1 has a total capacity of 7 (4+3), and S_2 has a total capacity of 6 (4+2). So, our minimum cut is 6, and we can send a maximum of 6 units of flow from to in :

Network Flow Saturated

6. Conclusion

In this article, we explained Menger’s theorem. It tells us that for an undirected graph with two non-adjacent vertices $\boldsymbol{u}$ and $\boldsymbol{v}$ , the minimum number of vertices needed to disconnect both of them is equal to the maximum number of the internally disjoint paths between $\boldsymbol{u}$ and $\boldsymbol{v}$ .

Persistence

REST

Security