1. Introduction
In this tutorial, we consider hashing techniques used in various data structures that provide constant time access to their elements.
We discuss in more detail the so-called folding technique and give a short introduction to mid-square and binning techniques.
2. Overview
When we choose data structures for storing objects, one of the considerations is whether we need to access them quickly.
The Java utility package offers us quite a lot of data structures for storing our objects. For more information on data structures, refer to our Java Collections compilation page that contains guides on several of them.
As we know, some of these data structures allow us to retrieve their elements in constant time, independent of the number of elements that they contain.
Probably, the simplest one is the array. In fact, we access elements in the array by their index. The access time, naturally, does not depend on the size of the array. In fact, behind the scene, many data structures heavily use arrays.
The problem is that the array indexes must be numeric, while we often prefer to manipulate these data structures with objects.
In order to address this problem, many data structures try to assign a numeric value that can serve as an array index to objects. We call this value a hash value or simply a hash.
3. Hashing
Hashing is a transformation of an object into a numerical value. Functions that perform these transformations are called hash functions.
For the sake of simplicity, let’s consider hash functions that transform strings into array indexes, that is, into integers from the range [0, N] with a finite N.
Naturally, a hash function is applied to a wide variety of strings. Therefore its “global” properties become important.
Unfortunately, it’s not possible that a hash function always transforms different strings into different numbers.
We may convince ourselves quite easily that the number of strings is much bigger than the number of integers in any range [0, N]. Therefore, it’s inevitable that there is a pair of non-equal strings for which a hash function produces equal values. This phenomenon is called collision.
We are not going to dive into the engineering details behind hash functions, but it’s clear that a good hash function should try to map uniformly the strings on which it’s defined into numbers.
Another obvious requirement is that a good hash function should be fast. If it takes too long to calculate a hash value, then we cannot access elements quickly.
In this tutorial, we consider one of the techniques that try to make the mapping uniform while maintaining it fast.
4. Folding Technique
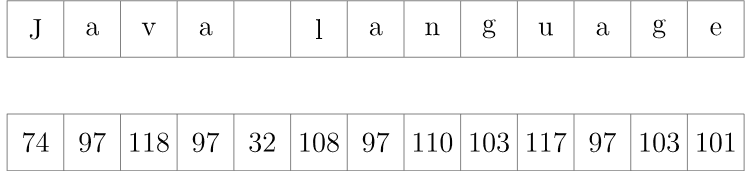
Our goal is to find a function that transforms strings into array indexes. Just to illustrate the idea, suppose that we want this array to have the capacity for 105 elements and let’s use string Java language as an example.
4.1. Description
Let’s start by converting the string’s characters into numbers. ASCII is a good candidate for this operation:
Now, we arrange the numbers we just obtained into groups of some size. Generally, we choose the group size value based on the size of our array which is 105. Since the numbers, in which we transformed the characters into, contain from two to three digits, without loss of generality, we may set the group size to two:
The next step is to concatenate the numbers in each group as if they were strings and find their sum:
Now we must make the final step. Let’s check whether the number 348933 may serve as an index of our array of size 105. Naturally, it exceeds the maximum allowed value 99999. We may easily overcome this problem by applying the modulo operator in order to find the final result:
348933 % 10000 = 48933
4.2. Final Remarks
We see that the algorithm does not include any time-consuming operations and hence it is quite fast. Every character of the input string contributes to the final result. This fact definitely helps to reduce collisions, but not to avoid them completely.
For example, if we wanted to skip the folding and applied the modulo operator directly to the ASCII-transformed input string (ignoring the overflow issue)
749711897321089711010311797103101 % 100000 = 3101
then such hash function would produce the same value for all strings that have the same last two characters as our input string: age, page, large, and so on.
From the description of the algorithm, we can easily see that it is not free from the collisions. For instance, the algorithm produces the same hash value for Java language and vaJa language strings*.*
5. Other Techniques
The Folding Technique is quite common, but not the only one. Sometimes, the binning or mid-square techniques may be useful too.
We illustrate their idea by not using strings, but numbers (suppose that we have already somehow transformed the strings into numbers). We won’t discuss their advantages and weaknesses, but you may form an opinion after seeing the algorithms.
5.1. Binning Technique
Suppose that we have 100 integer numbers and we want our hash function to map them into an array of 10 elements. Then we may just arrange those 100 integers into ten groups in such a way that the first ten integers end up in the first bin, the second ten integers end up in the second bin, etc.:
5.2. Mid-Square Technique
This algorithm was proposed by John von Neumann and it allows us to generate pseudo-random numbers starting from a given number.
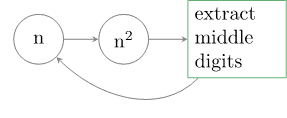
Let’s illustrate it on a concrete example. Suppose, we have a four-digit number 1111. According to the algorithm, we square it, thus obtaining 1234321. Now, we extract four digits from the middle, for example, 2343. The algorithm allows us to repeat this process until we are satisfied with the result.
6. Conclusion
In this tutorial, we considered several hashing techniques. We described in detail the folding technique and gave a flash description of how binning and mid-square can be achieved.
As always, we may find the corresponding code snippets on our GitHub repository.