1. 简介
二叉树是一种层次结构,其中每个节点最多有两个子节点。每个二叉树节点包含三个元素:一个数据字段保存整数值,两个子节点指针分别指向左子节点和右子节点。在本教程中,我们将使用前序遍历算法来解决一个二叉树路径和问题。
2. 二叉树路径和问题
给定一个二叉树的 root 节点和一个整数 targetSum,我们希望找出并打印所有满足路径和为 targetSum 的路径。路径不需要从根节点开始,也不必以叶子节点结束,但必须是自上而下的路径(即从父节点到子节点的路径)。
此外,单个节点也可以构成路径,只要其值等于 targetSum。例如,在下面的二叉树中,有 4 条路径满足 targetSum = 7:
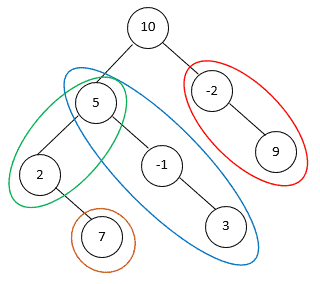
在极端情况下,比如整棵树的节点值都是 0,且 targetSum 也为 0,则我们需要打印所有可能的自上而下路径。
3. 前序遍历路径和序列
我们可以记录从根节点到当前节点的路径和,如下图所示:
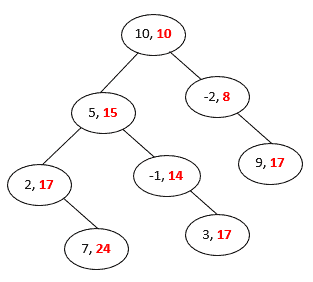
我们使用前序遍历算法来构建路径和序列:
- 先访问当前节点
- 再递归访问左子树
- 最后访问右子树
这样可以确保路径始终是向下的。例如,该二叉树的前序路径和序列为:
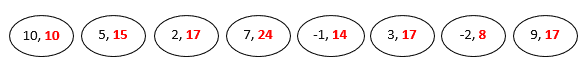
每个元素包含两个部分:
class PathSumNode {
TreeNode node; // 当前节点
int sum; // 从根到当前节点的路径和
}
✅ 前序遍历生成路径和代码如下:
public List<PathSumNode> preOrderPathSum(TreeNode root) {
List<PathSumNode> sequence = new ArrayList<>();
pathSumRecursive(root, 0, sequence);
return sequence;
}
private void pathSumRecursive(TreeNode node, int sum, List<PathSumNode> sequence) {
if (node == null) return;
sum += node.val;
sequence.add(new PathSumNode(node, sum));
pathSumRecursive(node.left, sum, sequence);
pathSumRecursive(node.right, sum, sequence);
}
该算法时间复杂度为 **O(n)**,因为我们每个节点只访问一次。
4. 打印所有路径和等于 targetSum 的路径
基于前序遍历得到的路径和序列,我们可以快速计算任意两个节点之间的路径和:
路径和 =
sequence[j].sum - sequence[i].sum + sequence[i].node.val
例如,在示例中计算节点 5 到节点 3 的路径和为:17 - 15 + 5 = 7
✅ 打印所有符合条件路径的算法如下:
public void printAllPathsWithTargetSum(List<PathSumNode> sequence, int targetSum) {
for (int i = 0; i < sequence.size(); i++) {
for (int j = i; j < sequence.size(); j++) {
int pathSum = sequence.get(j).sum - sequence.get(i).sum + sequence.get(i).node.val;
if (pathSum == targetSum) {
printPath(sequence.get(i).node, sequence.get(j).node);
}
}
}
}
✅ 打印路径的方法如下:
public boolean printPath(TreeNode source, TreeNode target) {
List<Integer> path = new ArrayList<>();
if (findPath(source, target, path)) {
System.out.println(path);
return true;
}
return false;
}
private boolean findPath(TreeNode node, TreeNode target, List<Integer> path) {
if (node == null) return false;
path.add(node.val);
if (node == target) return true;
if (findPath(node.left, target, path) || findPath(node.right, target, path)) {
return true;
}
path.remove(path.size() - 1);
return false;
}
⚠️ 时间复杂度分析:
- 构建路径和序列:O(n)
- 遍历所有节点对:O(n²)
- 每次打印路径:O(n)
因此,总时间复杂度为 **O(n³)**,适用于中等规模的树结构。
5. 小结
在本教程中,我们介绍了如何通过前序遍历构建路径和序列,并基于该序列找出所有满足目标和的路径。虽然最终算法的时间复杂度为 O(n³),但其逻辑清晰、实现简单,适用于树结构不是特别大的场景。
如果你对性能有更高要求,可以考虑使用哈希表 + 回溯的方法优化到 O(n²),这将在后续文章中介绍。