1. 引言
在本文中,我们将展示如何找出一组二维点中曼哈顿距离最小的那对点。
2. 曼哈顿距离简介
假设我们有一组二维点:
$$ Z = {z_i}_{i=1}^{n}, z_i = (x_i, y_i), i = 1, 2, \ldots, n $$
我们希望找到曼哈顿距离(Manhattan Distance)最小的那对点。
曼哈顿距离是指只能沿水平和垂直方向移动时,两点之间的最短路径长度。如下图所示:
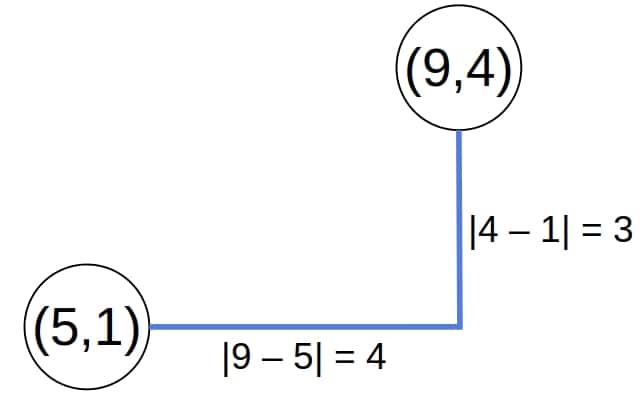
其计算公式为:
$$ d_{M} \left( (x_i, y_i), (x_j, y_j)\right) = |y_j - y_i| + |x_j - x_i| $$
3. 算法设计
最直接的做法是暴力枚举所有点对,计算每对之间的曼哈顿距离,然后找出最小值。但这种方法的时间复杂度是 $O(n^2)$,效率较低。
为了提升性能,我们可以使用 分治策略(Divide and Conquer) 来解决这个问题。
3.1 分治策略思路
我们将点集 $Z$ 用一条垂直线分割成左右两部分 $P$ 和 $Q$:
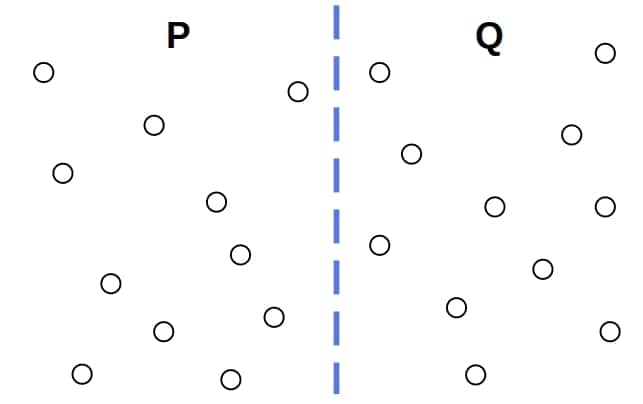
那么,最小曼哈顿距离的点对可能出现在以下三种情况之一:
- 两点都在 $P$ 中
- 两点都在 $Q$ 中
- 一个点在 $P$,另一个点在 $Q$
我们递归地求解 $P$ 和 $Q$ 中的最小距离,分别记为 $\delta_P$ 和 $\delta_Q$,取 $\delta = \min(\delta_P, \delta_Q)$。
接着,我们只需要检查那些横跨分割线、且距离小于 $\delta$ 的点对。
我们只需要关注位于分割线两侧 $\delta$ 范围内的点,这些点组成的区域称为 strip(条带):
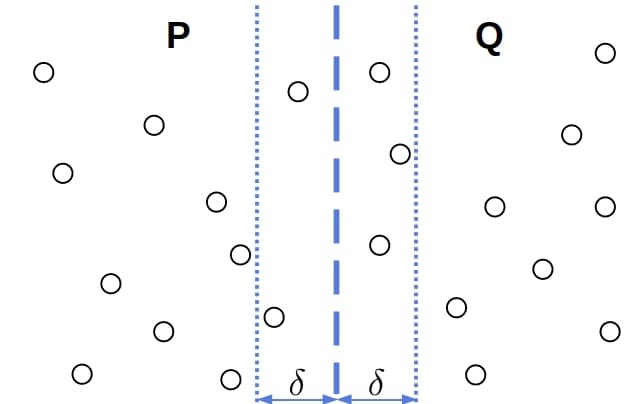
在这个 strip 中,我们检查每对点的距离,找出最小值 $\delta'$,最终的最小距离就是 $\min(\delta, \delta')$。
3.2 时间复杂度分析
设 $T(n)$ 为处理 $n$ 个点所需的时间,$f(n)$ 表示划分点集和查找 strip 中最小距离的时间。
则有递推式:
$$ T(n) = 2 T \left( \frac{n}{2} \right) + f(n) $$
如果 $f(n) = O(n)$,则总时间复杂度为 $O(n \log n)$。
但如果我们在 strip 中暴力枚举所有点对,则 $f(n) = O(n^2)$,整体时间复杂度退化为 $O(n^2)$,与暴力法无异。
因此,我们关键要做的,是在 strip 中快速找出最小距离。
3.3 Strip 的结构特性
在 strip 中,我们只关注那些横跨分割线的点对。设当前最小距离为 $\delta$,则在 strip 中,点对之间的垂直距离必须小于 $\delta$。
我们可以在 strip 中将点按 $y$ 坐标排序,然后对于每个点,只需要检查其后最多 9 个点即可:
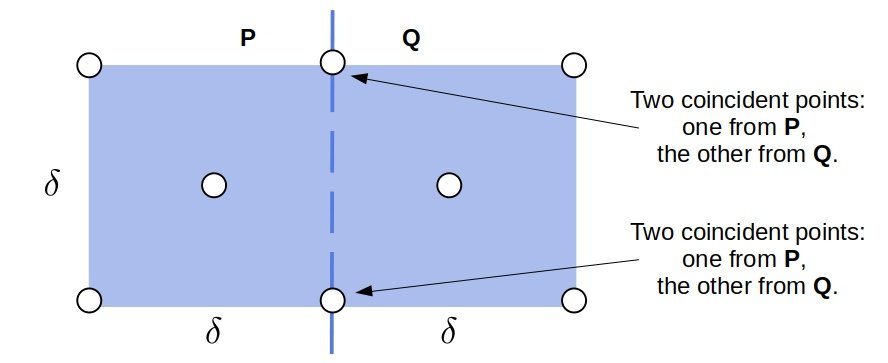
这样,我们可以在 $O(n)$ 时间内完成 strip 中的最小距离查找。
3.4 预排序优化
为了在递归中快速获取 strip 中的点并按 $y$ 排序,我们可以在最开始就对点集进行预排序:
- 一份按 $x$ 坐标排序(用于划分点集)
- 一份按 $y$ 坐标排序(用于 strip 中快速查找)
每次递归时,我们通过线性时间的合并操作(类似归并排序)来拆分排序数组,这样可以保证分治过程的时间复杂度仍为 $O(n \log n)$。
3.5 算法伪代码
algorithm FindClosest(Z, X, Y):
// Z: 原始点集
// X: 按 x 排序的点集
// Y: 按 y 排序的点集
// 返回最小曼哈顿距离和对应的点对
if n <= 1:
return ∞, null
if n <= 3:
// 手动计算所有点对
return bruteForceFindClosest(Z)
P, Q <- split Z into left and right halves by x
X_P, X_Q <- split X into P and Q
Y_P, Y_Q <- split Y into P and Q
delta_P, pair_P <- FindClosest(P, X_P, Y_P)
delta_Q, pair_Q <- FindClosest(Q, X_Q, Y_Q)
delta <- min(delta_P, delta_Q)
best_pair <- delta_P < delta_Q ? pair_P : pair_Q
strip <- filter Y to keep only points within delta of the dividing line
for each point p in strip:
for next 9 points q after p:
d <- manhattan(p, q)
if d < delta:
delta <- d
best_pair <- (p, q)
return delta, best_pair
3.6 曼哈顿距离的特殊性
我们之所以能在 strip 中只检查每个点后最多 9 个点,是因为曼哈顿距离的几何特性决定了在一个 $2\delta \times \delta$ 的矩形中最多只能容纳 6 个点(每侧最多 3 个)。
如果我们使用的是欧几里得距离(Euclidean Distance),则最多可以容纳 8 个点,因此需要检查最多 7 个后续点。
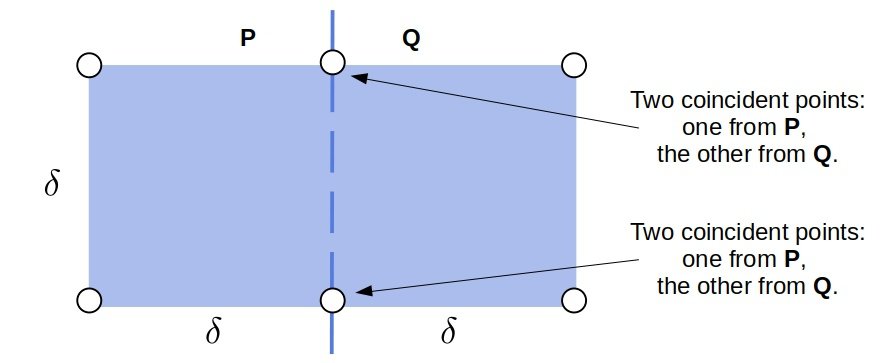
所以,不同距离函数会影响 strip 中点对的检查次数,但整体分治结构不变。
4. 总结
本文介绍了如何使用分治策略在 $O(n \log n)$ 时间内找出一组二维点中曼哈顿距离最小的那对点。
核心要点包括:
✅ 使用分治策略减少时间复杂度
✅ 利用 strip 结构优化跨区域点对查找
✅ 预排序和线性时间拆分确保整体效率
✅ 曼哈顿距离的几何特性决定了 strip 中最多只需检查每个点后 9 个点
这种算法是计算几何中的经典问题之一,具有广泛的应用价值。