链表上的快速排序：挑战是什么？

1. Introduction

Quicksort is a divide-and-conquer algorithm that sorts a sequence by recursively partitioning it around a pivot element.

In this tutorial, we’ll explore how to implement Quicksort for linked lists.

2. Solution With Using Extra Space

Let’s take a look at the implementation that uses auxiliary lists in the partitioning step:

algorithm QuickSort(list):
    // INPUT
    //    list = the linked list to sort
    // OUTPUT
    //    linked list sorted in the non-decreasing order
    if list is empty or has only one element:
        return list
    pivot <- select the pivot from the list

    smaller <- an empty list
    equalOrLarger <- an empty list
    current <- list.head.next

    while current is not null:
        if current.value < pivot:
            append current.value to smaller
        else:
            append current.value to equalOrLarger
        current <- current.next
 
    smaller <- QuickSort(smaller)
    equalOrLarger <- QuickSort(equalOrLarger)
    sortedList <- extend smaller with equalOrLarger
    return sortedList

We don’t spend much time dealing with pointers, but we take additional memory due to creating new sublists at every stage of the partitioning process.

3. In-Place Solution

Without auxiliary sublists, we need to swap the values within the original list:

algorithm QuickSort(list):
    // INPUT
    //    list = the linked list to sort
    // OUTPUT
    //    linked list sorted in the non-decreasing order
    if list is empty or has only one element:
        return list

    pivot <- list.head.value
    pivotPointer <- list.head
    current <- list.head.next

    while current is not null:
        if current.value < pivot:
            pivotPointer <- pivotPointer.next
            temp <- pivotPointer.value
            pivotPointer.value <- current.value
            current.value <- temp
        current <- current.next

    list.head.value <- pivotPointer.value
    pivotPointer.value <- pivot

    if list.head is not pivotPointer:
        left_head <- list.head
        left_end <- list.head
        while left_end.next is not pivotPointer:
            left_end <- left_end.next
        left_end.next <- null
        Quicksort(left_head)
        left_end.next = pivotPointer

    if pivotPointer.next is not null:
        right_head = pivotPointer.next
        Quicksort(right_head)
        pivotPointer.next = right_head

    return list.head

Implementing the in-place method ensures a constant space complexity because we avoided creating new sub-lists at every stage of the sorting process.

4. Challenges

Both approaches face the same challenges.

The primary challenge with linked lists stems from their lack of efficient random access. Reaching the -th element requires traversing over all the predecessors.

Further, with arrays, we can randomly select any element as the pivot in time, but with lists, selecting the element is of the . To have an selection, we have to settle for always choosing the first element as the pivot. This strategy increases the worst-case complexity to .

Also, lists can be non-contiguous, so traversing them can be inefficient, especially if memory blocks with list items must often be swapped into the main memory.

Let’s consider a simple example of a singly linked list with ten elements:

   

Now, let’s say we always choose the first element as the pivot:

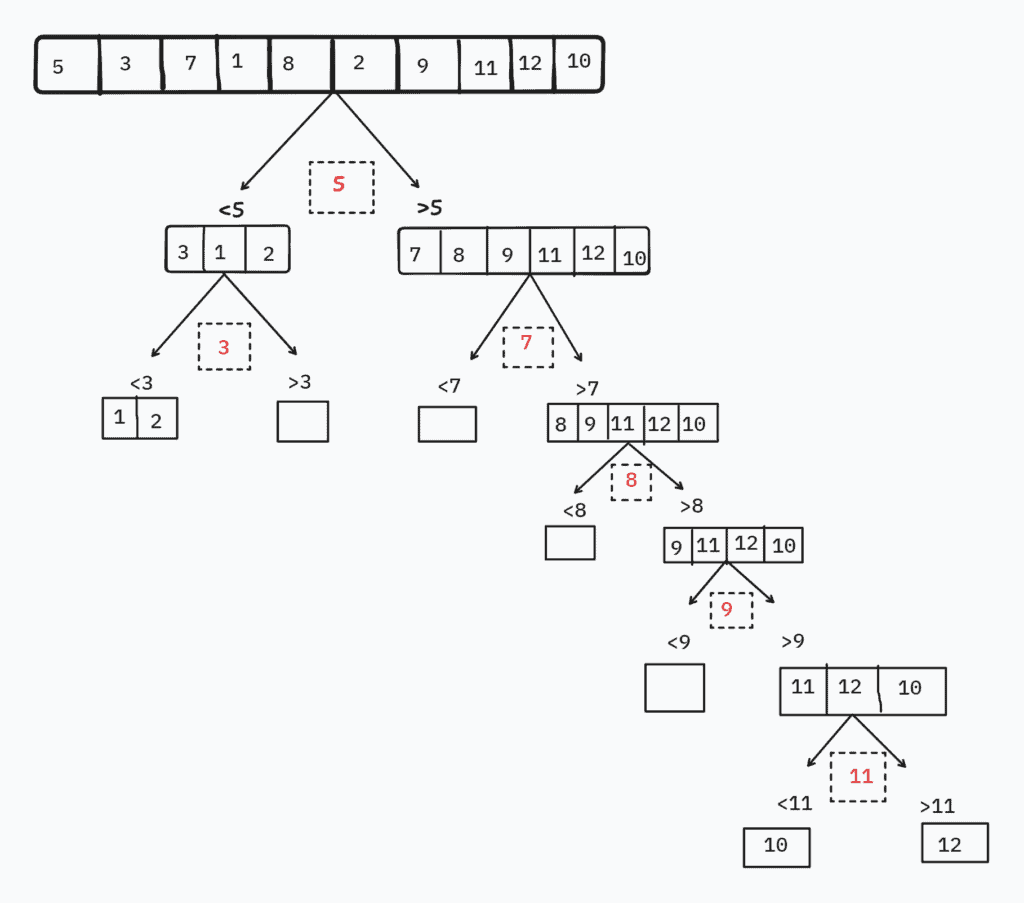
During the partitioning step, we swap values and rearrange pointers between nodes. This can lead to scattered memory access patterns and may cause additional overhead:

As we traverse the list to partition it, we constantly move back and forth to access elements in different memory blocks.

5. An Solution

Quicksort efficiency and time complexity depend highly on the pivot element we use in partitioning. Selecting the first element as the pivot leads to the worst-case complexity of if the list is already in the opposite order.

A robust strategy to improve the complexity is to use a pivot close to the median node. This strategy is commonly referred to as the median-of-medians technique. In it, we split the list into blocks of consecutive elements and calculate the blocks’ medians. Then, we compute the medians’ median and use it as the pivot. This way, partitioning returns non-empty left and right parts, so we avoid the worst-case complexity.

For instance:

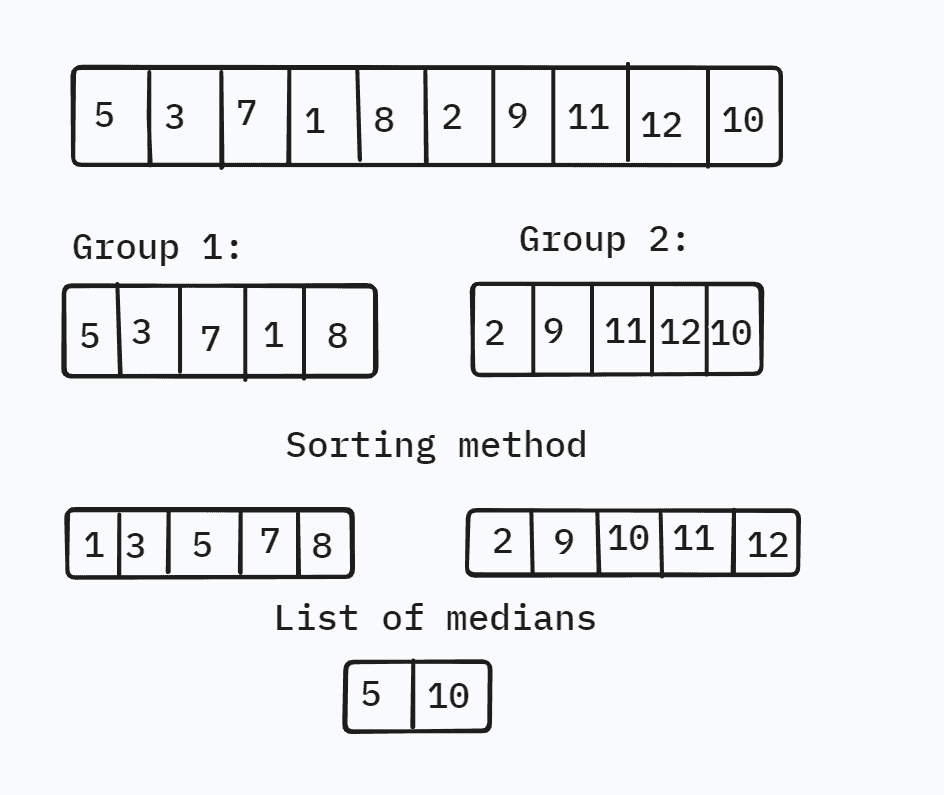
We have ten different nodes in this example, so we can split the list into two groups, each containing five nodes. The next step is to find the median node in each group. To do this, we can use selection sort due to its simplicity and efficiency in handling short sequences to sort the nodes in the group. Each group’s median will then be in the middle. Once we have the medians from the group, we will arrange them into a new list and recursively use QuickSelect to find the median in time. As a result, the worst-case complexity becomes .

6. Conclusion

In this article, we discussed some of the challenges of implementing Quicksort for linked lists and how to mitigate them. Although the inherent characteristics of linked lists make it difficult to select a good pivot, we can use the median-of-medians technique to get a log-linear worst-case time complexity.